Tag Archives: Laminova

How COOL is THIS: Intercooler Pressure versus Pump Output and Flow @Motorama

Posted on by
2

Update:

Although the info shown is relevant for 4 Laminova cores in series, the Cadillac design does not have 4 in series but rather has A-B in parallel and C-D in parallel flow.  I caused some confusion in the way I asked my question of Laminova as it turns out.  I am leaving this for consideration, but the pressure head through 2 Laminova cores instead of through 4 cores would be different.

 

Intercooler coolant pumps are at heart 12v water pumps.  Extra points if they are light and quiet, and very long lasting.  They are rated in gallons per minute, or liters per minute, or liters per hour.  However, with pumps one also has to know at what pressure.  If an 8 gpm pump is pumping against NO resistance then it can pump 8 gpm of fluid.  However, if it is pumping against some resistance, like the four cores of a STS-V intercooler, it has a harder job and the flow rate will drop.

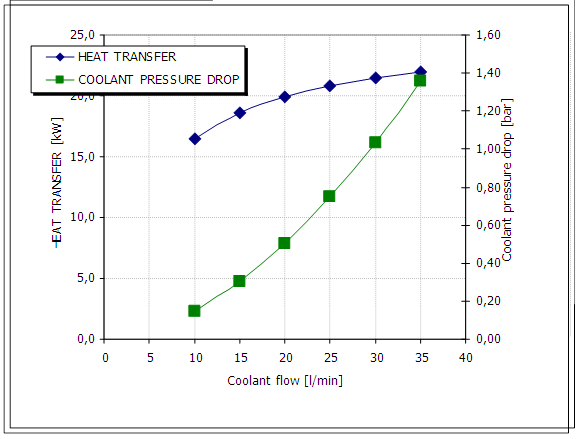
Laminova was kind enough to send me this graphic showing pressure versus flow through four Laminova cores sized for the Cadillac STS-V application in serial:

Below is a graph with heat transfer vs. flow rate for a 4 x 39.5 mm cores in 392 mm length, coolant in series over the cores. (calculated with 350g/s 110ºC for the charge air, 30ºC coolant with flow from 10 to 35 l/min). As you can see performance continues to increase with increased flow, but at 35 l/min you have almost 1,4 bar pressure drop, then add the radiator etc. So be careful when choosing pump, normally there are graphs for flow vs. backpressure for the pumps available.

Laminova Cores bar of pressure vs lpm of flow

Let’s examine this graphic.  First, a bar of pressure is a bit less than the English atmosphere (A), so 1 atm (atmosphere) = 1.01325 bar.  Let’s stay in bar for now, as it is frequently used for discussion of our topic.  But when you read bar you can think 14.5 psi if you prefer.  A liter per minute is 0.2642 gallons per minute (gpm).

What the graphic shows is that as the coolant flow increases from 10 lpm (2.6 gpm) to 35 lpm (9 gpm) the pressure required to push the water through the 4 STS-V Laminova intercooler cores increases from 0.15 bar (2.1 psi) to 1.4 bar (20 psi).  It takes a LOT of pressure to reach a 9 gpm flow rate.  The good news is the heat transfer for the system of cores continues to improve right up to 9 gpm, flattening out after that rate of flow.

If we could increase the flow rate from 16 lpm (4 gpm) up to 35 lpm (9.2 gpm), the heat transfer will increase from around 16 kw up to around 22 kw, or 38% more intercooling at max rate.

It is inviting to think then, that the STS-V 8 gpm intercooler pump is about right on the money; unfortunately, that pressure it has to pump against lowers its output quite a bit.  Let’s see how much.

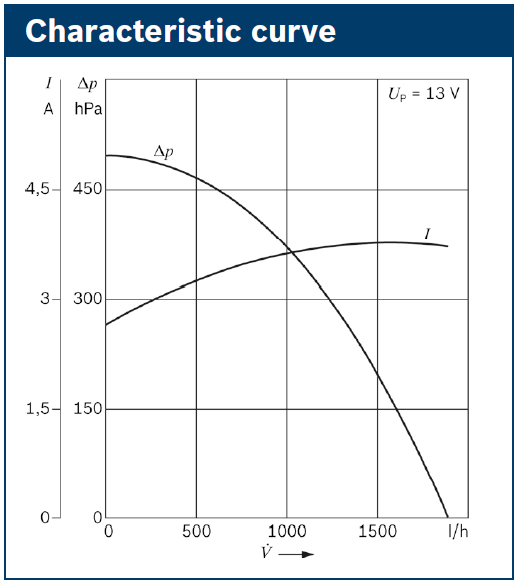
The Cadillac STS-V uses a Bosch sourced 8 gpm (gallon per minute) pump.  Here is a diagram of the Bosch pump output:

Bosch Intercooler Pump Flow vs Pressure

This diagram introduces new units again, but we’ll get through it.  Along the x axis we have Volume of flow in liters per hour.  Along the y axis we have delta pressure in hPa, which is hectopascals of pressure.  1000 hectopascals  = 1 bar.

So this Bosch pump will flow 0 liters per hour at 0.5 bar, and up to 1800 liters per hour (30 lpm, 7.9 gpm) at no pressure.  Good, as it is rated for 8 gpm.

Now, how do we determine how much a Bosch pump in our STS-V would flow against the pressure through the intercooler, hoses, and heat exchanger?  We graph them together based on flow rates versus pressure and see where their graphs cross.   That will be the point where the flow rate of the pump against the resistance in the system is equivalent.

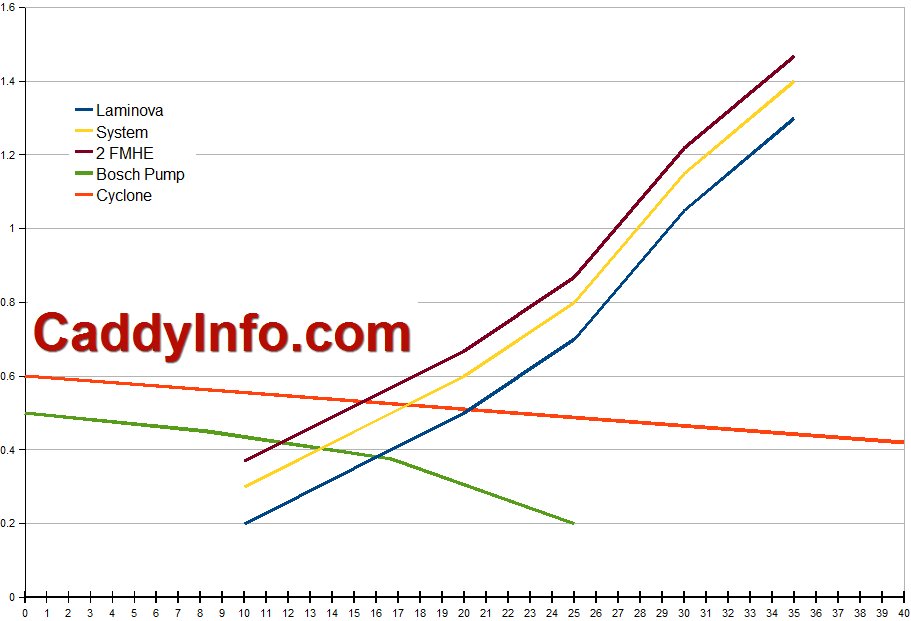
I have included the Jabsco 50840-12 Cyclone aftermarket intercooler pump for comparison as well, reading off their flow graphic.  This is a popular replacement intercooler pump for the STS-V.

Laminova System Cyclone Bosch Pump
FLOW L/Min Pressure bar Flow L/Min Pressure Bar Flow L/Min Pressure bar
10 0.20 0.3 0 0.6 0 0.5
15 0.35 0.45 40 0.42 8.33 0.45
20 0.50 0.6 80 0.2 16.67 0.38
25 0.70 0.8 120 0 25 0.2
30 1.05 1.15
35 1.30 1.4

This data table shows the resistance through the Laminova cores alone, then an equivalent resistance value for the whole intercooler cooling system.  I don’t know a good value for this so I used 0.1 bar or 1.4  psi of pressure to represent the intercooler heat exchanger (1 psi), hoses (0.4 psi), etc.  We can change it to another more accurate value later, and can model 2 heat exchangers, etc.

The data is really easy to relate to if we put each set on an XY graph, so let’s do that!

Calculated Flow Rates:

Cadillac STS-V Intercooler Flow Rate vs Pump Output & Pressure - Bar versus Liters per Minute

So reading from the graph, I find this tabular result:

Liters/Min Gallons/Min
Pump Core Only System Core only System
Bosch 16 13 4.19 3.41
Cyclone 20 18 5.24 4.72

In other words,  the 8 gpm Bosch pump will pump 4 gpm if it were only pumping through the 4 Laminova cores in serial (theoretical value), or 3.4 gpm through the whole system.

The higher flow Cyclone pump will or 4.7 gpm through the whole system, or 38% better than the stock pump.

A second FMHE (front mounted heat exchanger) might cost 1 psi and thus 2 lpm or 0.5 gpm of flow.  Also notable is that the Cyclone pump with a 2nd FMHE still probably flows more than the stock pump and single FMHE.  Heat transfer probably increases by 0.5 kw, or 38% of the increased flow rate of 1.3 gpm.

Ideas for further study:

Design an experiment to test actual flow rate through the system.  Ideal to me would be to add a flow rate indicator (gauge).

Source a replacement intercooler coolant pump that can pump 9 gpm against a 1.5 bar head pressure in order to optimize intercooler cooling.  This is likely to need to be a positive displacement pump rather than a centrifugal pump.

See an error?   Applause for the effort?  Chime in via the comments section!!

@Cadillac STS-V Supercharger & Intercooler Ideas #Motorama

Posted on by
2

The Cadillac STS-V (2006-2009) featured the 4.4L DOHC VVT LC3 V8 with a custom Eaton M122 Supercharger and integrated intercooler.

This photo shows the Cadillac LC3 engine without the ‘beauty cover’, looking from the rear of the engine — so the front of the Cadillac would be right and away.

Air flows in the black tubes at the top of the engine to the ‘back’ of the engine, and into the supercharger.  Note the noise baffles in the intake tubing intended to isolate the whine of the supercharger.

This view is of the supercharger+intercooler from the back:

 

and the next view is the reverse angle or ‘front facing’ shot of the coolant in/out tubes flowing to the intercooler (black part).  The ‘snout’ is the drive for the supercharger.  A belt runs from a pulley below to turn the Supercharger, pressurizing the incoming air.

Once you open and separate the supercharger and intercooler they look like this — note the intercooler is flipped upside down here, as if you simply removed it by ‘opening it up’:

STS-V Intercooler removed from Supercharger

The intercooler is an air to water system, and features Laminova laminar flow heat exchange tubes.

The air flows into the back of the supercharger through the long intake.  Then it is pumped up from the center of the supercharger through the intercooler past the Laminova tubes, and then it flows down the sides of the intercooler casing and the supercharger casing and into the engine.

Each of the four Laminova tubes look like this up close:

Laminova STS-V Intercooler Tubes

The science of the Laminova design is to create huge surface area with minimal air flow restriction.  The very thin fins, 0.2 mm each, along each Laminova tube collect the heat from the air passing through the 0.3 mm gaps between the fins.  The surface area presented to the air flow is approximately 5 times greater than a conventional plate-style intercooler according to Laminova, as well as reducing noise and pulsation.

The heat is conducted to channels surrounding the solid core of each Laminova tube, where liquid coolant is passing through to remove it.

It appears that the coolant flows into the intercooler, circulates through all 4 Laminova intercooler tubes, and then flows back to the intercooler heat exchanger.  The heat exchanger is like a small radiator.  The intercooler coolant system is completely separate from the engine cooling system/radiator.

The advantage of the Laminova design is that they have a very good efficiency with low pressure disruption and light weight.   A disadvantage is cost.

The CTS-V LSA engine uses a finned box air to water intercooler:

This shot shows the CTS-V LSA intercooler upside down.

How can the STS-V intercooler be improved?

An interesting ‘science project’ for the STS-V intercooler would be to replace the intercooler endcaps that direct coolant flow through one Laminova core after another with a custom endcap that directed coolant flow in parallel with all 4 Laminova cores and out after one pass.

One expert mentions that it is helpful to ‘index’ the 4 Laminova cores, so that the large fins are facing the air flow.  I am not clear looking at the images what is intended, as the Laminova cores appear to be uniform and symmetrical, unless the intent is to rotate the ‘sleeves’ the cores are contained in?

Owners are also experimenting with larger heat exchangers at the other end of the system, larger fluid reservoirs to allow more fluid to circulate and absorb heat, and higher capacity intercooler coolant pumps to circulate fluid.

On the slots that allow flow across the Laminova tubes, are the cross-pieces structurally needed?  If removed, so that the slots were just continuous single slots — flow would be increased.

Do you see other avenues to explore?